Considerando n um número natural maior que 1 (um), podemos definir como fatorial desse número n (n!) o número:
n! = n(n – 1)(n – 2)(n – 3) * ...* 3 * 2 * 1
Lê-se n! como n fatorial ou fatorial de n.
Veja alguns exemplos:
5! = 5 * 4 * 3 * 2 * 1 = 120
8! = 8 * 7 * 6 * 5 * 4 * 3 * 2 * 1 = 40320
6! = 6 * 5 * 4 * 3 * 2 * 1 = 720
10! = 10 * 9 * 8 * 7 * 6 * 5 * 4 * 3 * 2 * 1 = 3.628.800
VÍDEO AULA SOBRE FATORIAL
Princípio Fundamental da Contagem
Quando um evento é composto por n etapas sucessivas e independentes, de tal forma que as possibilidades da primeira etapa é m e as possibilidades da segunda etapa é n, consideramos então que o número total de possibilidades de o evento ocorrer é dado pelo produto m*n.
Ao lançarmos uma moeda e um dado temos as seguintes possibilidades:
Moeda: cara ou coroa (duas possibilidades)
Dado: 1, 2, 3, 4, 5, 6 (seis possibilidades)
Observando o ocorrido, vemos que o evento tem duas etapas com 2 possibilidades em uma e 6 em outra, totalizando 2*6 = 12 possibilidades.
Exemplo 2
Quantos números de 3 algarismos podemos escrever com os algarismos 2, 4 e 6? E de algarismos distintos?
Podemos escrever 3 * 3 * 3 = 27 números de 3 algarismos.
Três algarismos distintos: 3 * 2 * 1 = 6 números de 3 algarismos distintos.
Arranjo Simples
A análise combinatória estuda dois tipos de agrupamentos: Arranjos e combinações. Sendo que diferem em arranjos simples, combinações simples.
Arranjos são agrupamentos nos quais a ordem dos seus elementos faz a diferença. Por exemplo, os números de três algarismos formados pelos elementos {1, 2 e 3} são:
312, 321, 132, 123, 213, 231
Esse agrupamento é um arranjo, pois a ordem dos elementos 1, 2 e 3 diferem. E é considerado simples, pois os elementos não se repetem.
Para que tenhamos arranjos simples é preciso ter um conjunto de elementos distintos com uma quantidade qualquer de elementos, sendo que os arranjos simples formados irão possuir n elementos, sendo que essa quantidade será igual ou menor que a quantidade de elementos do conjunto.
Veja o exemplo abaixo:
Dado o conjunto B = {5,6,7}, veja os possíveis agrupamentos formados com 2 elementos de B.
Então, os agrupamentos formados com 2 elementos do conjunto b são: 56,57,65,67,75,76. Esse agrupamento é formado por arranjos simples pelos elementos do conjunto B.
Nesse exemplo percebemos que é possível formar 6 arranjos, essa quantidade pode ser representada da seguinte forma: A3,2 (três elementos distintos formados de dois a dois). Utilizando o processo do princípio fundamental da contagem, calculamos a quantidade de elementos:
A3,2 = 3 . 2 . 1 = 6
Se em um agrupamento compararmos os arranjos simples formados perceberemos que eles se diferem de duas maneiras diferentes: pela ordem de seus elementos ou pela natureza de seus elementos. Por exemplo:
Se compararmos os arranjos 56 e 65 do exemplo anterior, perceberemos que eles são diferentes pela ordem dos seus elementos.
Se compararmos os arranjos 75 e 76 do exemplo anterior, perceberemos que eles são diferentes pela natureza de seus elementos, pois são diferentes.
Considerando n a quantidade de elementos de um conjunto qualquer e p um número natural menor ou igual a n. p será a classe ou a ordem do arranjo. Indicado da seguinte forma: A n , p
A fórmula geral utilizada no cálculo da quantidade de arranjos simples é:
.jpg)
Exemplo 2:
Quantas “palavras” (com sentido ou não) de 5 letras distintas podemos formar com as 20 primeiras letras do nosso alfabeto?
Não é necessário montar todas os arranjos possíveis para saber a sua quantidade, basta aplicar a fórmula:
A n , p = n!
(n – p)!
Sendo que o conjunto é formado por 20 elementos (n = 20) que serão unidos de 5 em 5 (p = 5). Substitua a fórmula.
.jpg)
Portanto, a quantidade de arranjos formados com as 20 primeiras letras do nosso alfabeto unidas de 5 em 5 é 1860480.
Permutação Simples
Podemos considerar a permutação simples como um caso particular de arranjo, onde os elementos formarão agrupamentos que se diferenciarão somente pela ordem. As permutações simples dos elementos P, Q e R são: PQR, PRQ, QPR, QRP, RPQ, RQP. Para determinarmos o número de agrupamentos de uma permutação simples utilizamos a seguinte expressão P = n!.
n! = n*(n-1)*(n-2)*(n-3)*....*3*2*1
Por exemplo, 4! = 4*3*2*1 = 24
Exemplo 1
n! = n*(n-1)*(n-2)*(n-3)*....*3*2*1
Por exemplo, 4! = 4*3*2*1 = 24
Exemplo 1
Quantos anagramas podemos formar com a palavra GATO?
Resolução:
Podemos variar as letras de lugar e formar vários anagramas, formulando um caso de permutação simples.
P = 4! = 24
.jpg)
Resolução:
Podemos variar as letras de lugar e formar vários anagramas, formulando um caso de permutação simples.
P = 4! = 24
.jpg)
Exemplo 2
De quantas maneiras distintas podemos organizar as modelos Ana, Carla, Maria, Paula e Silvia para a produção de um álbum de fotografias promocionais?
Resolução:
Note que o princípio a ser utilizado na organização das modelos será o da permutação simples, pois formaremos agrupamentos que se diferenciarão somente pela ordem dos elementos.
P = n!
P = 5!
P = 5*4*3*2*1
P = 120
Portanto, o número de posições possíveis é 120.
Exemplo 3
De quantas maneiras distintas podemos colocar em fila indiana seis homens e seis mulheres:
a) em qualquer ordem
Resolução
Podemos organizar as 12 pessoas de forma distinta, portanto utilizamos
12! = 12*11*10*9*8*7*6*5*4*3*2*1 = 479.001.600 possibilidades
b) iniciando com homem e terminando com mulher
Resolução
Ao iniciarmos o agrupamento com homem e terminarmos com mulher teremos:
Seis homens aleatoriamente na primeira posição.
Seis mulheres aleatoriamente na última posição.
.jpg)
P = (6*6) * 10!
P = 36*10!
P = 130.636.800 possibilidades
P = 36*10!
P = 130.636.800 possibilidades
Combinação Simples
Na combinação simples, a ordem dos elementos no agrupamento não interfere. São arranjos que se diferenciam somente pela natureza de seus elementos. Portanto, se temos um conjunto A formado por n elementos tomados p a p, qualquer subconjunto de A formado por p elementos será uma combinação, dada pela seguinte expressão:
.jpg)
Por exemplo, considere um conjunto com seis elementos que serão tomados dois a dois:
.jpg)
Uma importante aplicação de combinação simples é nas loterias, megassena, quina entre outras. A megassena consiste em uma cartela de 60 números dentre os quais devemos acertar 6 (prêmio principal), portanto temos uma combinação onde n = 60 e p = 6, sessenta números tomados seis a seis.
.jpg)
.jpg)
Na megassena existem 50.063.860 combinações, caso sejam tomadas seis a seis.
Em um curso de língua estrangeira estudam trinta alunos. O coordenador do curso quer formar um grupo de três alunos para realizar um intercâmbio em outro país. Quantas possíveis equipes podem ser formadas?
Resolução:
O número de possíveis grupos pode ser dado pela expressão:
.jpg)
Poderão ser formadas 4060 equipes.
VÍDEO AULA SOBRE ANÁLISE COMBINATÓRIA
Análise Combinatória:
http://www.youtube.com/watch?v=zBjw3Ws45NU (Parte 8 - Final)
Binômio de Newton
Introdução
Pelos produtos notáveis, sabemos que (a+b)² = a² + 2ab + b².
Se quisermos calcular (a + b)³, podemos escrever:
Se quisermos calcular (a + b)³, podemos escrever:
(a + b)3 = a3 + 3a2b + 3ab2 + b3
Se quisermos calcular 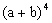 , podemos adotar o mesmo procedimento:
, podemos adotar o mesmo procedimento:
(a + b)4 = (a + b)3 (a+b) = (a3 + 3a2b + 3ab2 + b3) (a+b)
= a4 + 4a3b + 6a2b2 + 4ab3 + b4
De modo análogo, podemos calcular as quintas e sextas potências e, de modo geral, obter o desenvolvimento da potência 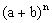 a partir da anterior, ou seja, de
a partir da anterior, ou seja, de 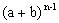 .
.
Porém quando o valor de n é grande, este processo gradativo de cálculo é muito trabalhoso.
Existe um método para desenvolver a enésima potência de um binômio, conhecido como binômio de Newton (Isaac Newton, matemático e físico inglês, 1642 - 1727). Para esse método é necessário saber o que são coeficientes binomiais, algumas de suas propriedades e o triângulo de Pascal.
Coeficientes Binomiais
Sendo n e p dois números naturais 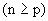 , chamamos de coeficiente binomial de classe p, do número n, o número
, chamamos de coeficiente binomial de classe p, do número n, o número 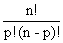 , que indicamos por
, que indicamos por 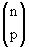 (lê-se: n sobre p). Podemos escrever:
(lê-se: n sobre p). Podemos escrever:
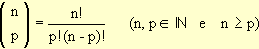 |
O coeficiente binomial também é chamado de número binomial. Por analogia com as frações, dizemos que n é o seu numerador e p, o denominador. Podemos escrever:
É também imediato que, para qualquer n natural, temos:
Exemplos:
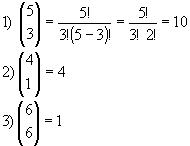 | 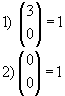 |
Propriedades dos coeficientes binomiais
1ª)
|
|
Coeficientes binomiais como esses, que tem o mesmo numerador e a soma dos denominadores igual ao numerador, são chamados complementares.
Exemplos:
2ª)
|
|
Essa igualdade é conhecida como relação de Stifel (Michael Stifel, matemático alemão, 1487 - 1567).
Exemplos:
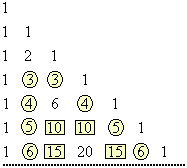
Triângulo de Pascal
| A disposição ordenada dos números binomiais, como na tabela ao lado, recebe o nome de Triângulo de Pascal | 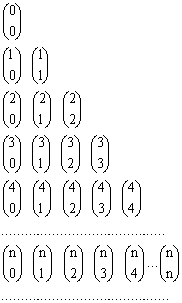 |
Por exemplo, os números binomiais
Substituindo cada número binomial pelo seu respectivo valor, temos:
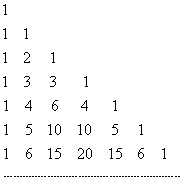
Construção do triângulo de Pascal
Para construir o triângulo do Pascal, basta lembrar as seguintes propriedades dos números binomiais, não sendo necessário calculá-los:
1ª) Como 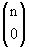 = 1, todos os elementos da coluna 0 são iguais a 1.
= 1, todos os elementos da coluna 0 são iguais a 1.
2ª) Como  = 1, o último elemento de cada linha é igual a 1.
= 1, o último elemento de cada linha é igual a 1.
3ª) Cada elemento do triângulo que não seja da coluna 0 nem o último de cada linha é igual à soma daquele
que está na mesma coluna e linha anterior com o elemento que se situa à esquerda deste último (relação
de Stifel).
que está na mesma coluna e linha anterior com o elemento que se situa à esquerda deste último (relação
de Stifel).
Observe os passos e aplicação da relação de Stifel para a construção do triângulo:
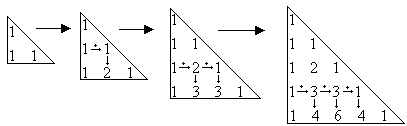
Propriedade do triângulo de Pascal
P1 Em Qualquer linha, dois números binomiais eqüidistantes dos extremos são iguais.
 | 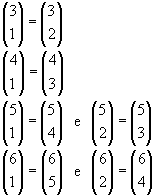 |
De fato, esses binomiais são complementares.
P2 Teorema das linhas: A soma dos elementos da enésima linha é 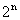 .
.
De modo geral temos:
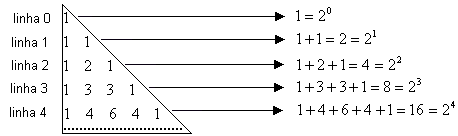
P3 Teorema das colunas: A soma dos elementos de qualquer coluna, do 1º elemento até um qualquer, é igual ao elemento situado na coluna à direita da considerada e na linha imediatamente abaixo.
 | 1 + 2 + 3 + 4 + 5 + 6 = 211 + 4 + 10 + 20 = 35 |
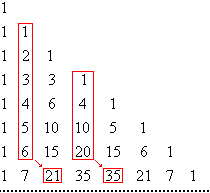
P4 Teorema das diagonais: A soma dos elementos situados na mesma diagonal desde o elemento da 1ª coluna até o de uma qualquer é igual ao elemento imediatamente abaixo deste.
 | 1 + 3 + 6 + 10 + 15 = 35 |
Fórmula do desenvolvimento do binômio de Newton
Como vimos, a potência da forma 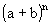 , em que a,
, em que a, 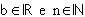 , é chamada binômio de Newton. Além disso:
, é chamada binômio de Newton. Além disso:
- quando n = 0 temos
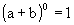
- quando n = 1 temos
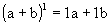
- quando n = 2 temos
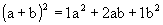
- quando n = 3 temos
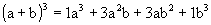
- quando n = 4 temos
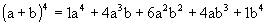
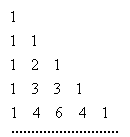
Observe que os coeficientes dos desenvolvimentos foram o triângulo de Pascal. Então, podemos escrever também:
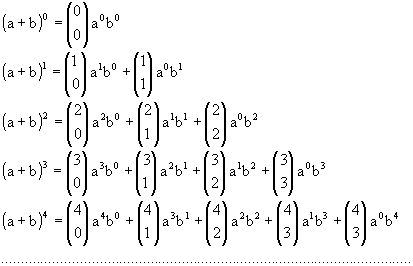
De modo geral, quando o expoente é n, podemos escrever a fórmula do desenvolvimento do binômio de Newton:
Note que os expoentes de a vão diminuindo de unidade em unidade, variando de n até 0, e os expoentes de b vão aumentando de unidade em unidade, variando de 0 até n. O desenvolvimento de (a + b)n possui n + 1 termos.
Fórmula do termo geral do binômio
Observando os termos do desenvolvimento de (a + b)n, notamos que cada um deles é da forma 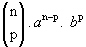 .
.
- Quando p = 0 temos o 1º termo:
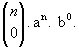
- Quando p = 1 temos o 2º termo:
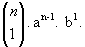
- Quando p = 2 temos o 3º termo:
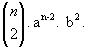
- Quando p = 3 temos o 4º termo:
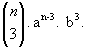
- Quando p = 4 temos o 5º termo:
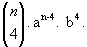
..............................................................................
Percebemos, então, que um termo qualquer T de ordem p + 1pode ser expresso por:
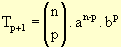 |
Binômio de Newton:
http://www.youtube.com/watch?v=Szy4v175hIo (Parte 7 - Final)
FONTE: VESTIBULANDIA, BRASIL ESCOLA E SÓ MATEMÁTICA


Nenhum comentário:
Postar um comentário