Apaixonado por Matemática: Conjuntos e Conjuntos Numéricos

Definição:

Conjunto é uma reunião de elementos, podemos dizer que essa definição é bem primitiva, mas a partir dessa ideia podemos relacionar outras situações. O conjunto universo e o conjunto vazio são tipos especiais de conjuntos.

Vazio: não possui elementos e pode ser representado por { } ou Ø.

Universo: possui todos os elementos de acordo com o que estamos trabalhando, pode ser representado pela letra maiúscula U.

Representando conjuntos

A representação de um conjunto depende de determinadas condições:

Exemplo 1

Condição: O conjunto dos números pares maiores que zero e menores que quinze.

Representação através de seus elementos.

A = {2, 4, 6, 8, 10, 12, 14}

Representação pela propriedade de seus elementos.

A = {x / x é par e 0 < x < 15}, o símbolo da barra (/) significa “tal que”.

x tal que x é par e x maior que zero e x menor que 15.

Exemplo 2

Condição: O conjunto dos números Naturais ímpares menores que vinte.

Elementos

A = {1, 3, 5, 7, 9, 11, 13, 15, 17, 19}

Propriedade dos elementos

A = {x Є N / x é impar e x < 20}

x pertence aos naturais tal que x é impar menor que 20.

Outra forma de representação de conjuntos de elementos é a utilização de diagramas. Observe os conjuntos A e B.

A = {x / 2 < x ≤ 12} e B = {x / 4 < x < 8}

União do conjunto A com o conjunto B. (A U B)

Os conjuntos servem para representar qualquer situação envolvendo ou não elementos. Na Matemática, uma importante aplicação dos conjuntos é na representação de conjuntos numéricos.

Conjunto dos números Naturais

Conjunto dos números Inteiros

Conjunto dos números Racionais

Conjunto dos números Irracionais

Conjunto dos números Reais

Conjunto dos números Complexos

Conjunto dos números Algébricos

Conjunto dos números Transcendentais

Conjunto dos números Imaginários

Os estudos básicos sobre conjuntos deram origem aos estudos relacionados às Teorias dos Conjuntos, que faz uma análise sobre as suas propriedades. Esses estudos se originaram nos trabalhos do matemático russo Georg Cantor. Na teoria dos conjuntos, os elementos podem ser: pessoas, números, outros conjuntos, dados estatísticos e etc.

Diagrama de Venn

Através de estudos relacionados à lógica, Jon Venn criou uma diagramação baseada em figuras no plano. Esse método consiste basicamente em círculos que possuem a propriedade de representar relações entre conjuntos numéricos. Também pode ser utilizado no estudo da Estatística, a fim de organizar e analisar dados colhidos em pesquisas de opinião. Geralmente usamos os seguintes modelos de diagramas:

Representação de conjunto único

Números Naturais (1, 2, 3, 4, 5, 6)

Relação entre dois conjuntos: A e B.

A = (1, 2, 3, 4, 5, 6)

B = (5, 6, 7, 8, 9, 10)

Símbolos

U = união

∩ = intersecção

A U B = (1, 2, 3, 4, 5, 6, 7, 8, 9, 10)

A ∩ B = (5, 6)

Relação entre três conjuntos: A, B e C.

A = (3, 4, 5, 6, 7, 8)

B = (4, 6, 8, 10, 12)

C = (1, 2, 3, 4, 6, 10)

A U B = (3, 4, 5, 6, 7, 8, 10, 12)

A U C = (1, 2, 3, 4, 5, 6, 7, 8, 10)

B U C = (1, 2, 3, 4, 6, 8, 10, 12)

A ∩ B = (4, 6, 8)

A ∩ C = (3, 4, 6)

C ∩ B = (4, 6, 10)

Podemos observar através dos exemplos que os diagramas representam de uma forma prática e eficiente as relações de união e de intersecção entre os conjuntos numéricos. Eles podem ser usados na representação de quaisquer conjuntos, no intuito de estabelecer uma melhor demonstração e compreensão dos elementos pertencentes ao conjunto.

Conjunto unitário e conjunto vazio

Por exemplo:

A = { x | x é par e 4 < x < 8 } ou A = {6}

B = { x | 2x + 1 = 7 e x é inteiro } ou B = {3}

Os dois conjuntos acima são exemplos de conjuntos unitários. Pois possuem apenas um elemento.

Dado o conjunto C = { y | y é natural e 2 < y < 3 } é um conjunto que não possui nenhum elemento, esse tipo de conjunto é chamado de conjunto vazio.

Indicamos um conjunto vazio por { } ou

, nunca por {

Igualdade de conjuntos

Dizemos que um conjunto é igual a outro se todos os elementos de um conjunto forem iguais a todos os elementos

do outro conjunto.

Exemplo:

Dados os conjuntos A = {0,1,2,3,4} e B = {2,3,4,1,0} como todos os elementos são iguais podemos dizer que A = B.

Relação entre dois conjuntos.

Quando vamos fazer a relação de elemento com conjunto utilizamos os símbolos de

pertence e

não pertence .

Por exemplo:

Dado o conjunto dos números naturais o elemento 5

N e -8

Agora quando relacionamos conjunto com conjunto utilizamos os símbolos de

está contido e

não está contido .

Por Exemplo:

{1,2,3}

{1,2,3,4,5,6}

O conjunto dos N está contido dentro dos inteiros. N

Z e o conjunto dos inteiros não está contido dentro do conjunto dos naturais Z

Interseção

Os elementos que fazem parte do conjunto interseção são os elementos comuns aos conjuntos relacionados.

Exemplo 1:

Dados dois conjuntos A = {5,6,9,8} e B = {0,1,2,3,4,5}, se pedimos a interseção deles teremos:

A ∩ B = {5}, dizemos que A “inter” B é igual a 5.

Exemplo 2:

Dados os conjuntos B = {-3, -4, -5, -6} e C = {-7, -8, -9}, se pedirmos a interseção deles teremos:

B ∩ C = { } ou B ∩ C =

, então B e C são conjuntos distintos.

Exemplo 3:

Dados os conjuntos D = {1,2,3,4,5} e E = {3,4,5}. A interseção dos conjuntos ficaria assim:

E ∩ D = {3,4,5} ou E ∩ D = E, pode ser concluído também que

União

Conjunto união são todos os elementos dos conjuntos relacionados.

Exemplo 1:

Dados os conjuntos A = { x | x é inteiro e -1 < x < 2} e B = {1,2,3,4} a união desses dois conjuntos é :

A U B = {0,1,2,3,4}

Exemplo 2:

Dados os conjuntos A = {1,2,3} e B = {1,2,3,4,5} a união desses conjuntos é:

A U B = {1,2,3,4,5}, nesse caso podemos dizer que A U B = B.

Diferença entre dois conjuntos.

Dados dois conjuntos A e B chama-se conjunto diferença ou diferença entre A e B o conjunto formado pelos elementos de A que não pertencem a B.

O conjunto diferença é representado por A – B.

Exemplo 1:

A = {1,2,3,4,5} e B = {3,4,5,6,7} a diferença dos conjuntos é:

A – B = {1,2}

Exemplo 2:

A = {1,2,3,4,5} e B = {8,9,10} a diferença dos conjuntos é:

A – B = {1,2,3,4,5}

Exemplo 3:

A = {1,2,3} e B = {1,2,3,4,5}a diferença dos conjuntos é:

A – B =

Exemplo 4:

Dados os conjuntos A = {1,2,3,4,5,6} e B = {5,6}, a diferença dos conjuntos é:

A – B = {1,2,3,4}. Como B

A podemos escrever em forma de complementar:

A – B =

_A B = {1,2,3,4}.

Conjunto numérico

Para desenvolver a matemática hoje estudada, inúmeras mudanças na organização de todos os conceitos matemáticos foram necessárias. A concepção dos conjuntos numéricos recebeu maior rigor em sua construção com Georg Cantor, que pesquisou a respeito do número infinito. Cantor iniciou diversos estudos sobre os conjuntos numéricos, constituindo, assim, a teoria dos conjuntos.

A construção de todos os conjuntos numéricos que hoje possuímos parte de números inteiros usados apenas para contar até os números complexos que possuem vasta aplicabilidade nas engenharias, nas produções químicas, entre outras áreas.

Definir conjunto é algo tão primitivo que se torna uma tarefa difícil. Entretanto, compreendemos conjunto como uma coleção de objetos, números, enfim, elementos com características semelhantes.

Sendo assim, os conjuntos numéricos são compreendidos como os conjuntos dos números que possuem características semelhantes. Nesta seção, a concepção desses conjuntos será abordada, visando à compreensão dos elementos que constituem cada um dos conjuntos numéricos.

Temos então os seguintes conjuntos numéricos:

Conjunto dos números Naturais ();
Conjunto dos números Inteiros ();
Conjunto dos números Racionais ();
Conjunto dos números Irracionais ();
Conjunto dos números Reais ();

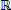Números Naturais

Pertencem ao conjunto dos naturais os números inteiros positivos, incluindo o zero. Esse conjunto é representado pela letra N maiúscula. Os elementos dos conjuntos devem estar sempre entre chaves.

N = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, ... }

- Quando for representar o Conjunto dos Naturais não nulos (excluindo o zero) devemos colocar * ao lado do N.

Representado assim:

N* = {1, 2,3 ,4 ,5 ,6 ,7 ,8 ,9 ,10 ,11 ,12, ... }

A reticência indica que sempre é possível acrescentar mais um elemento.

N = {0, 1, 2, 3, 4, 5, 6, ...} ou N = {0, 1, 2, 3, 4, 5, 6, 7, ... }

Qualquer que seja o elemento de N, ele sempre tem um sucessor. Também falamos em antecessor de um número.

• 6 é o sucessor de 5.

• 7 é o sucessor de 6.

• 19 é antecessor de 20.

• 47 é o antecessor de 48.

Como todo número natural tem um sucessor, dizemos que o conjunto N é infinito.

Quando um conjunto é finito?

O conjunto dos números naturais maiores que 5 é infinito: {6, 7, 8, 9, ...}

Já o conjunto dos números naturais menores que 5 é finito: {0, 1, 2, 3, 4}

Veja mais alguns exemplos de conjuntos finitos.

• O conjunto dos alunos da classe.

• O conjunto dos professores da escola.

• O conjunto das pessoas que formam a população brasileira.

Números Inteiros

Os números inteiros positivos foram os primeiros números trabalhados pela humanidade e tinham como finalidade contar objetos, animais, enfim, elementos do contexto histórico no qual se encontravam.

O conjunto dos números inteiros positivos recebe o nome de conjunto dos números naturais. Sendo ele:

={0,1,2,3,4,5,6…}

Enquanto que o conjunto dos números inteiros contempla também os inteiros negativos, constituindo o seguinte conjunto:

={…,-8,-7,-6,-5,-4,-3,-2,-1,0,1,2,3,4,5,6,7,8…}

Os números inteiros estão presentes até hoje em diversas situações do cotidiano da humanidade, como, por exemplo, para medir temperaturas, contar dinheiro, marcar as horas, etc. Sua importância é indiscutível.

Diante disso, buscaremos estudar todas as propriedades desse conjunto numérico que existe há tanto tempo, perpassando pela teoria de conjuntos, intersecção de conjuntos numéricos, entre outros conceitos que fazem parte desse conteúdo.

Números Racionais

Os números decimais são aqueles números que podem ser escritos na forma de fração.

Podemos escrevê-los de algumas formas diferentes:

Por exemplo:

♦ Em forma de fração ordinária:

;

e todos os seus opostos.

Esses números têm a forma

com a , b

Z e b ≠ 0.

♦ Números decimais com finitas ordens decimais ou extensão finita:

Esses números têm a forma

com a , b

Z e b ≠ 0.

♦ Número decimal com infinitas ordens decimais ou de extensão infinita periódica. São dízimas periódicas simples ou compostas:

As dízimas periódicas de expansão infinita podem ser escritas na forma

: com a, b

Z e b ≠ 0.

- O conjunto dos números racionais é representado pela letra Q maiúscula.

Q = {x =

, com a Z e b Z*}

- Outros subconjuntos de Q:

Além de N e Z, existem outros subconjuntos de Q.

Q^* ---------- É o conjunto dos números racionais diferentes de zero.

Q₊ ---------- É o conjunto dos números racionais positivos e o zero.

Q_- ----------- É o conjunto dos números racionais negativos e o zero.

Q_^*+ ---------- É o conjunto dos números racionais positivos.

Q^*_- ----------- É o conjunto dos números racionais negativos.

- Representação Geométrica

Entre dois números racionais existem infinitos outros números racionais.

Números Irracionais

Todo número decimal é um número irracional? Para as pessoas que têm dúvida quanto a isso, veremos, neste artigo, como definir o conjunto dos números irracionais e observaremos alguns exemplos de números importantes na matemática, que são “constantes irracionais”.

Os números irracionais são aqueles que não podem ser representados por meio de uma fração. O surgimento desses números veio de um antigo problema que Pitágoras se recusava a aceitar, que era o cálculo da diagonal de um quadrado, cujo lado mede 1 unidade, diagonal esta que mede √2. Este número deu início ao estudo de um novo conjunto, representado pelos números irracionais.

Encontrando a diagonal do quadrado

Hoje em dia, pensamos: “Nossa, mas encontrar o valor de √2 é tão fácil, basta usarmos a calculadora”. Entretanto, na época em que começaram estes estudos, o único mecanismo para encontrar os valores das raízes quadradas envolvia os números quadrados (√2²,√3²,√4², …).

Com o estudo contínuo dos elementos da matemática, os matemáticos se depararam com a necessidade de calcular o comprimento de uma circunferência; e com cálculos contínuos, notaram que um número se repetia para qualquer que fosse a circunferência, número este que outrora foi denominado de número pi (π).

Esse número é encontrado através da razão do comprimento pelo diâmetro da circunferência.

Esse é um dos números que foi citado no início do texto: a constante π é de fundamental importância para a área de geometria e trigonometria.

Veremos alguns exemplos de números irracionais e notaremos que a sua parte decimal não possui nenhuma estrutura que possa ser fundamentada em forma de fração, assim como ocorre em frações periódicas.

Constantes irracionais ou números transcendentais:

Números irracionais obtidos pela raiz quadrada de um número:

Números irracionais obtidos pela radiciação

Estes são os números irracionais, cujo valor da última casa decimal nunca saberemos.

Com isso, podemos falar que números irracionais são aqueles que em sua forma decimal são números decimais infinitos e não periódicos. Em outras palavras, são aqueles números que possuem infinitas casas decimais e em nenhuma delas obteremos um período de repetição.

O conjunto dos números irracionais é representado pela letra I ( i maiúscula) .

Números Reais

O conjunto dos números reais surge para designar a união do conjunto dos números racionais e o conjunto dos números irracionais. É importante lembrar que o conjunto dos números racionais é formado pelos seguintes conjuntos: Números Naturais e Números Inteiros. Vamos exemplificar os conjuntos que unidos formam os números reais. Veja:

Números Naturais (N): 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, ....
Números Inteiros (Z): ..., –8, –7, –6, –5, –4, –3, – 2, –1, 0, 1, 2, 3, 4, 5, 6, 7, 8, .....
Números Racionais (Q): 1/2, 3/4, 0,25, –5/4,
Números Irracionais (I): √2, √3, –√5, 1,32365498...., 3,141592....

Podemos concluir que o conjunto dos números reais é a união dos seguintes conjuntos:

N U Z U Q U I = R ou Q U I = R

Os números reais podem ser representados por qualquer número pertencente aos conjuntos da união acima. Essas designações de conjuntos numéricos existem no intuito de criar condições de resolução de equações e funções. As soluções devem ser dadas obedecendo padrões matemáticos e de acordo com a condição de existência da incógnita na expressão.

Símbolos

: pertence	: existe
: não pertence	: não existe
: está contido	: para todo (ou qualquer que seja)
: não está contido	: conjunto vazio
: contém	N: conjunto dos números naturais
: não contém	Z : conjunto dos números inteiros
/ : tal que	Q: conjunto dos números racionais
: implica que	Q'= I: conjunto dos números irracionais
: se, e somente se	R: conjunto dos números reais